…als ob Betti neben dir in der Vorlesung sitzt, so lang du sie brauchst!

Deine ersten Mathe Semester auf einen Klick:
Jedes Thema wird ausführlich Schritt für Schritt von Betti im Mathe Intensivkurs erklärt. Im Anschluss eines jeden Themas gibt es 3-7 Übungen zur Kontrolle.
Während allen Modulen siehst und hörst du Betti - als wäre sie neben dir. Deine Fragen kannst du jederzeit in deine Gruppe stellen. Wir sind jederzeit für dich da
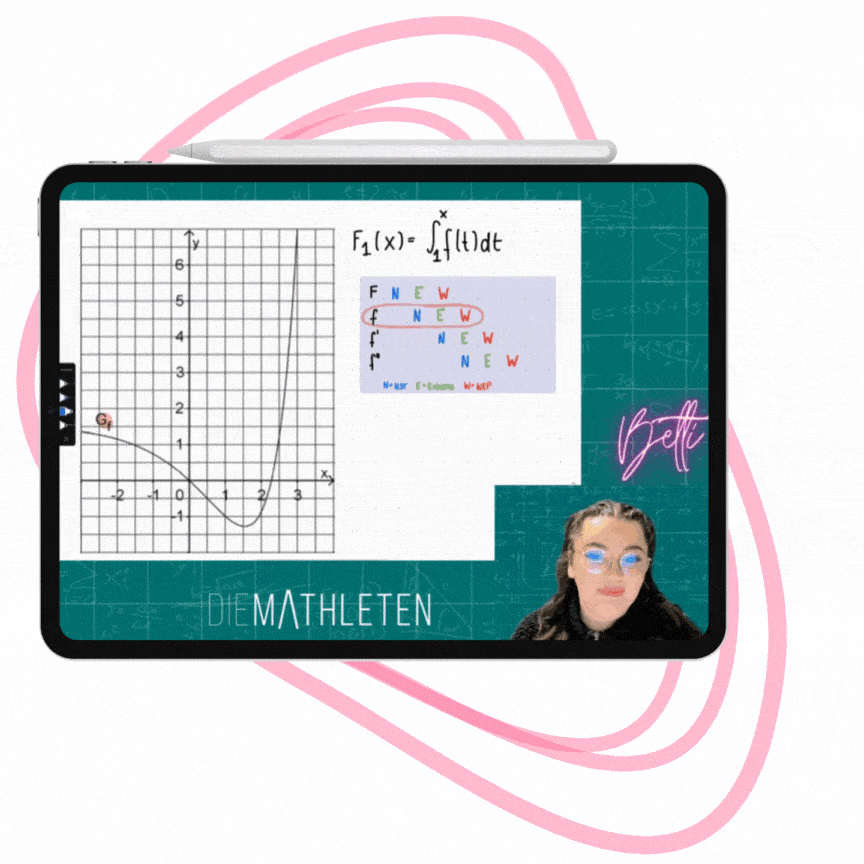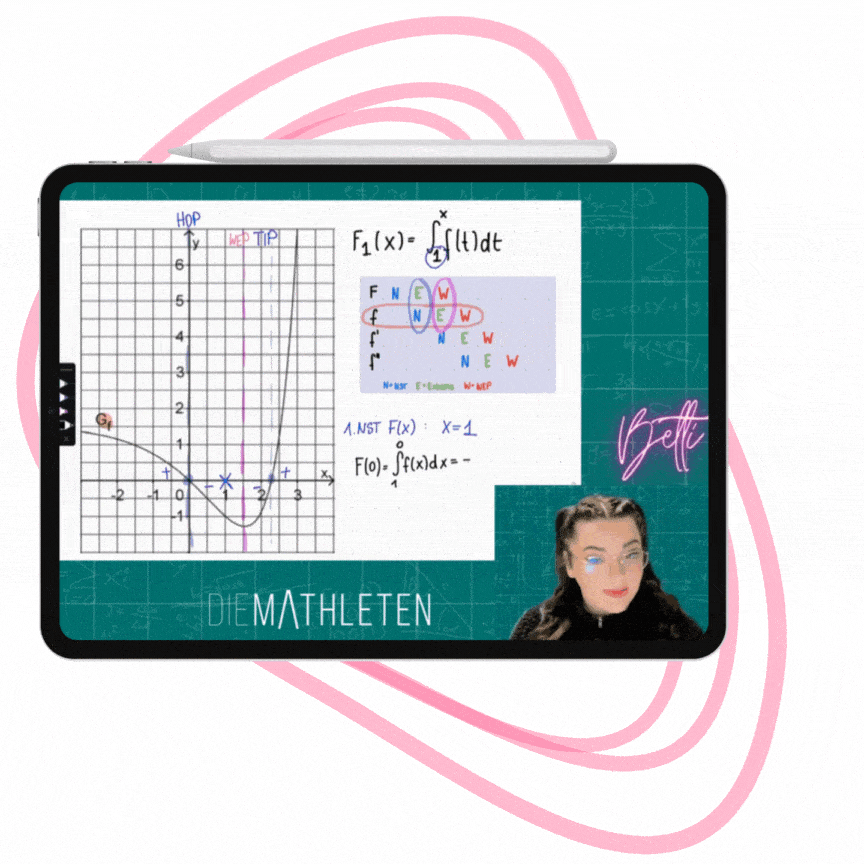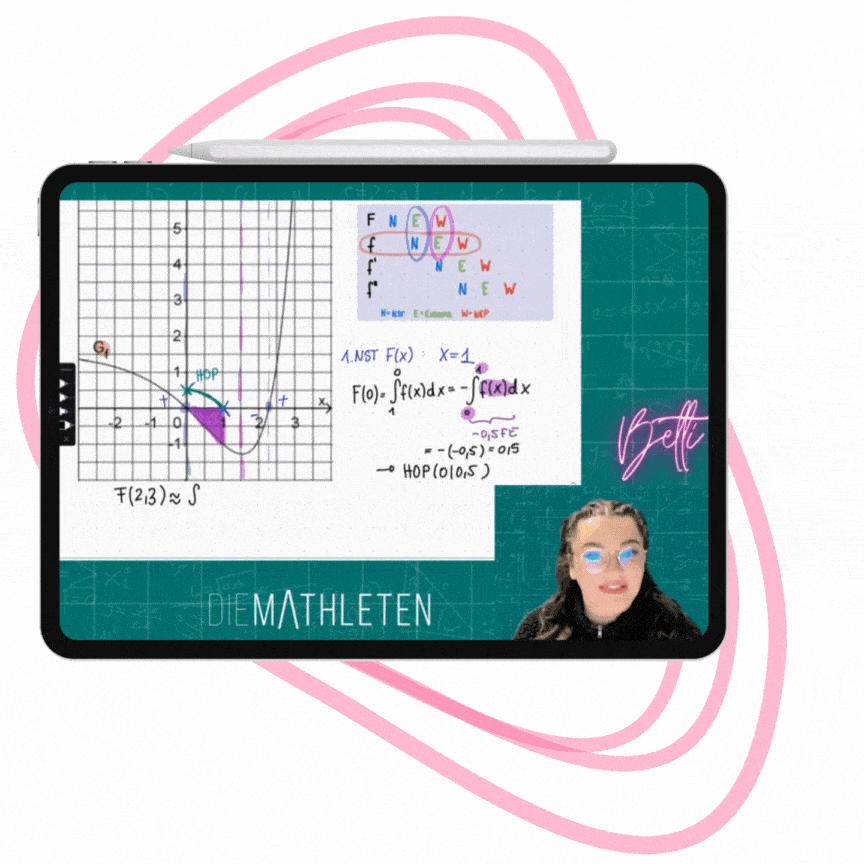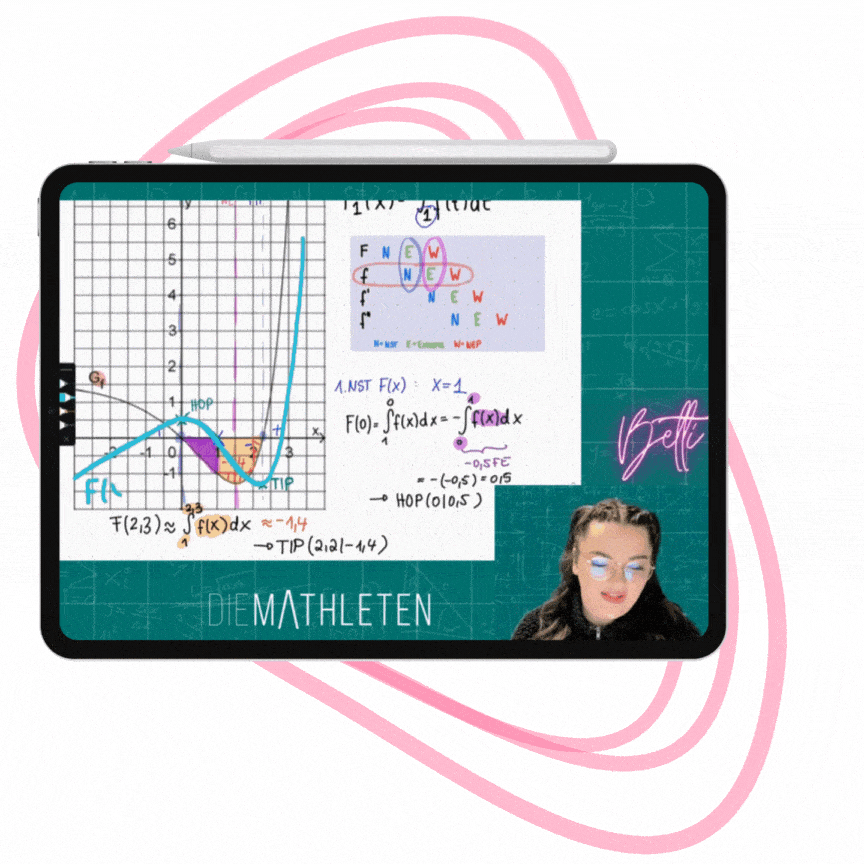
Das virtuelle Whiteboard ist im selben Programm, in dem auch unsere Bücher erstellt worden sind - genau so farbig, und genau so verständlich!
Zu jeder Einheit gibt es die Kursfolien und Übungen zum Download (leer & ausgefüllt) – so kannst du diese ausdrucken, oder parallel zum Video am Tablet mitschreiben

Im Laufe des Semesters werden wir die Themen deiner kommenden Mathe Klausur in unserer Lernplattform erklärt.
Inkl. Vorkurs!

Also außer wenn wir schlafen 😀
Ansonsten gilt:
Betti
unterstützt dich
bei jeder Frage und
Turoriums-Aufgabe!

Erhalte wertvolle Tipps zum Lernen, Zeitmanagement,
im Studium,
und die Klausurvorbereitung
an der Uni!

Schritt-für-Schritt Rechnungen von
4 Probeklausuren!
So bist du bestens gewappnet.
Grundlagen der Algebra:
– Potenz & Logarithmus Regeln
– Gleichungen
– Ungleichungen
Zu Beginn:
– Vollständige Induktion
– Komplexe Zahlen
Folgen & Reihen:
– Folgen & Reihen
– Folgenkonvergenz und epsilon Kriterium
– Reihenkonvergenz und Konvergenzradius
Funktionen und Grenzverhalten:
– Geraden
– tanzrationale Funktionen
– Wurzelfunktionen
– e-Funktionen
– ln – Funktionen
– Betragsfunktion en
– Gebrochenrationale Funktionen
– Sinus und Cosinus Funktionen
– Umkehrfunktionen
– Symmetrie
– Definitionsbereich
– Limes & L`Hospital
Differentialrechnung:
– Differentialquotient
– Stetigkeit & Differenzierbarkeit
– Höhere Ableitungsregeln
– Taylorentwicklung
– Extrema & Monotonie
– WEP & Krümmung
– Newtonverfahren
Riemann Integral:
– Stammfunktion der Grundfunktionen
– Lineare Verkettung & Substitution
– für gebrochen rationale Funktionen
– partielle Integration
– partialbruchzerlegung
Analysis mehrerer Veräderlichen:
– Höher dimensionale Extrema: Gradient & Hesse Matrix
– Lagrange Optimierung
Grundlagen:
– Vektorrechnung
– Gaußverfahren
– Dimension, Basis, EZS, kern einer Matrix
Matrix Rechnung:
– Rechnen mit Matrizen
– Determinante & Cramer
– Inverse
Eigenwerte & Diagonalisiertbarkeit
Im Kurs enthalten:
für monatlich nur
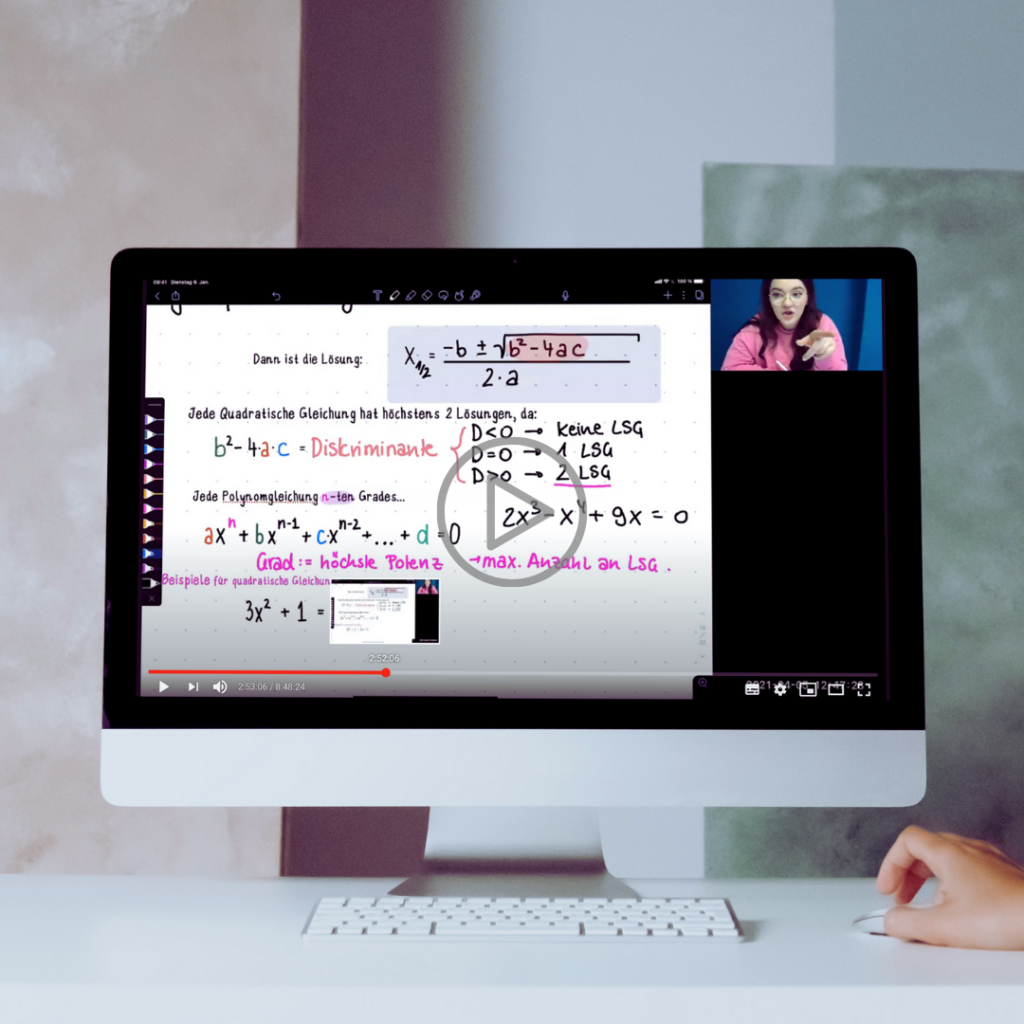
Bettis oberste Priorität in unseren Kursen ist, dass wirklich jedes Thema behandelt wird – und das auch noch so, dass es wirklich zu deiner Mathe Vorlesung passt!
Jede Universität, jeder Studiengang sogar jeder Professor innerhalb einer Uni gestaltet seine Mathe Vorlesung unterschiedlich.
Die Themen unterscheiden sich dabei, sind allerdings aus einem typischen Themen-Pool.
In der Liste Oben hast du eine Übersicht aller Themen, die im Laufe des Semesters von Betti behandelt werden.
Mit unserer Lernplattform hast du die Möglichkeit, dir die Inhalte so einzuteilen, wie du möchtest – und wann du möchtest.
Was du schon drauf hast, kannst du überspringen.
So kannst du dir Zeit sparen und selbst entscheiden, in welchem Tempo du lernst – deine Fragen können dabei jederzeit in deiner Support-Gruppe beantwortet werden.

Die Interaktion mit dir ist Betti extrem wichtig – genauso wie die Tatsache, dass du immer die Möglichkeit hast, Fragen zu stellen, damit nichts ungeklärt bleibt.
Aus diesem Grund gibt es unsere
Mathe-Fragen Support-Gruppe.
In dieser Gruppe ist Betti und das ganze Mathleten-Team – und außerdem alle Teilnehmer:innen.
Hier kannst du Betti im Rahmen deines Abos jederzeit Fragen zu Inhalten, Tutorien- & Klausur-Aufgaben usw. stellen – die sie beantwortet.
Und ihr könnt euch außerdem auch zu anderen Vorlesungen, dem Uni-Leben austauschen und Zusammenfassungen dazu verschicken. Diese Gruppen sind jedes Jahr eine riesige Bereicherung für alle Teilnehmer:innen!
Im Intensivkurs geht es vor allem um’s Verständnis – hier wird dir Betti eine Schritt-für-Schritt Anleitung für die Themen der ersten Mathe-Vorlesungen geben.
Am Ende jeder Theorie-Einheit gibt es eine Übung mit 1-5 Aufgaben zu dem jeweiligem Thema, die didaktisch ausgewählt wurden, damit du das Thema zu 100% verstehst.
Im Januar geht es dann ans Klausuren Training:
Hier rechnen wir an zwei Wochenenden verschiedene Altklausuren damit du perfekt vorbereitet bist.
Außerdem:
Haben wir auch noch einen Alt-Klausur Pool mit Lösungen – um noch mehr Üben zu können.


Seit der Gründung ist uns eins besonders wichtig: Dass wir endlich allen zeigen können, dass Mathe das einfachste aller Schulfächer ist!
Diese Mission zeigt sich jedes Jahr in unseren Kursen, der Nachhilfe und unseren Mathe Abi Skripte:
Mathe IST einfach!
Wenn du eine Freundin an deiner Seite hast, die dir das zeigt, was sie sieht: diese Freundin ist Betti jährlich für hunderte Schüler:innen.
Sie ist wie die Freundin, die dir ihre schönen Zusammenfassungen schickt, dir kurz vor der Kurzarbeit 5 Std Unterricht in 5 Minuten erklärt – und dir auch mitten in der Nacht auf deine verzweifelte Nachricht antwortet, weil du einen Vorzeichenfehler gemacht hast.Sie weiß wie die Prüfungen erstellt und gewertet sind, was der Erwartungshorizont ist, was der didaktische Hintergrund ist, und was im Abi auf dich zukommen wird.
Mit diesem Wissen sind wir unübertroffen, denn:
MIT UNS KANNST DU RECHNEN!

So lang du möchtest!
Wir halten nichts von ekligen Langzeit-Abo Fallen. Du kannst den Intensivkurs immer zum Monatsende kündigen und auch wieder jederzeit buchen.

Wir haben in den letzten Jahren seit der Gründung riesige Erfolge feiern dürfen - und das hat einen einfachen Grund:
dein Lern-Erfolg und deine Zufriedenheit sind uns super wichtig!
In allem was wir tun, steht für uns dein Mathe-Erfolg wirklich an erster Stelle. Das merkst du an unseren Kursen und, Bettis kostenlosen Instagram Lives, den Skripten, usw.
Kaum eine andere Person kann bei der Mathematik-Expertise von Betti mithalten – und auch didaktisch ist sie unschlagbar. Mach dir selbst ein Bild davon!

JA! Betti liebt es, euch den Abitur-Stoff zu vermitteln und zu erklären, und dabei auf die ganzen unnötigen Randinfos und Herleitungen zu verzichten, die häufig in der Uni manchmal das Verständnis nur unnötig erschweren.

Der Kurs ist für alle geeignet, die ihre Bestleistung in ihrer Mathe-Vorlesung erzielen wollen.
Wir wissen, dass die erste Mathe-Vorlesung ein Schock sein kann. Die Hohen Durchfallquoten, die Beweis-lastigkeit, allein schon die "Sprache": Das schreckt viele am Anfang ab.
Wir wollen erreichen, dass Mathe dein kleinstes Probem ist!

Kurze Antwort: ja!
Je nach Hochschule (ob z.B. privat) kann es aber sein, dass der Kurs zu viele Themen behandelt - die du gar nicht behandeln wirst.
Dann ist ggf. einer unserer Abitur-Kurse sinnvoller.
Kontaktiere uns am besten mit dem Vorlesungsverzeichnis - dann können wir dir genau sagen welcher unserer Kurse zu dir passt.

Spaß, das hat noch keiner gefragt 😅 Es ist aber tatsächlich so: der Kurs ist aus unserer Sicht besser (und dazu auch noch auch günstiger) als gängiger Einzelunterricht.
Warum? Weil dir - unserer bescheidenen Meinung nach - keine Einzelnachhilfe auf dem Markt diese Struktur, und so viele und so hochwertige Inhalte und Benefits bieten kann. Und das alles von Bayerns wohl bester Mathe-Abi-Expertin: Betti weiß, welche Aufgaben wahrscheinlich in deiner nächsten Schulaufgabe dran kommen werden, und sie weiß auch, auf was es im Abi ankommt. Sie kennt den Lehrplan in- und auswendig, und kann dich daher auf alles vorbereiten, was dich dieses Schuljahr und im Abi erwarten wird!

Wir sind

und mit uns kannst du rechnen!
Nachdem Betti 2018 während ihres Mathematik & Physik Bachelor an der LMU einen schönen Mathe Traum hatte mit der Vision – die Mathematik so schön, einfach und bunt zu zeigen, wie sie für sie immer schon war – hat sie sich ihre Lieblingsmenschen für ihr Lieblingsfach ins Boot geholt und
DIE MATHLETEN waren geboren:
Raphi: das Mastermind und Bettis Partner
Bigu: das Productmind und Bettis Mama
Rosalie: das Projectmind und Bettis Bestie
Betti: das Mathemind